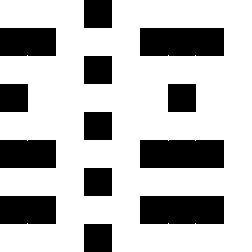Color Differential Geometry or the Spatial Color Model
Introduction
This webpage gives an overview of color scalespace or the spatial color model as it can be used in
digital image processing, from digital microscopy and
High Content Screening (HCS)
to medical imaging and astronomy.
Although this article is limited to 2D, the spatial color approach can be used for 3D and even 4D image processing.
Scalespace stacks (dimension, scale, order) can also
be used in convolutional neural networks, such as in the
M5 framework for exploring the cytome.
The basic principle is "what you describe is what you get".
For an introduction on differential geometry see
differential geometry. The spatial color model and linear and non linear scalespace
can be combined to select shapes with specific colors.
This webpage was inspired by the pioneering work on High Content Screening and
microscopy at the now defunct
Biological Imaging laboratory (BIL) at
Janssen Pharmaceutica in Beerse (Belgium).
Spatial color model
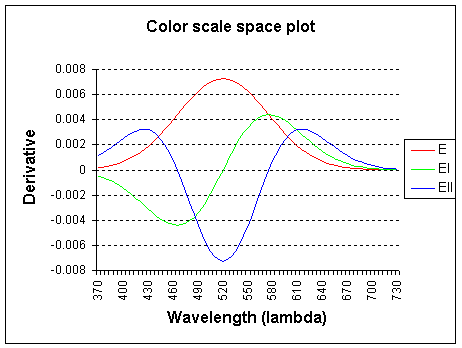
The graph shows the wavelength lambda (l) x-axis and the color derivatives, up to the second order.
E (intensity) is the 0th order derivative, El is the 1st order derivative to
f and Ell is the 2nd order derivative to f (f, frequency).
The spectrum is probed with a Gaussian kernel, centered on 520 nm and with sigma 55.0.
Note: the color derivatives are calculated relative to frequency, but plotted
to wavelength for convenience.
The 0th order (E) derivative measures the total weight of the light spectrum and corresponds closely
to the luminositiy curve as defined by the CIE 164 standard (standard human observer).
The 1st order derivative (El) of the spectrum measures
yellow-ish minus cyan-ish and the
2nd order derivative (Ell) measures green-ish minus
magenta-ish.
Higher-order derivatives are possible with multispectral systems (more than 3 channels).
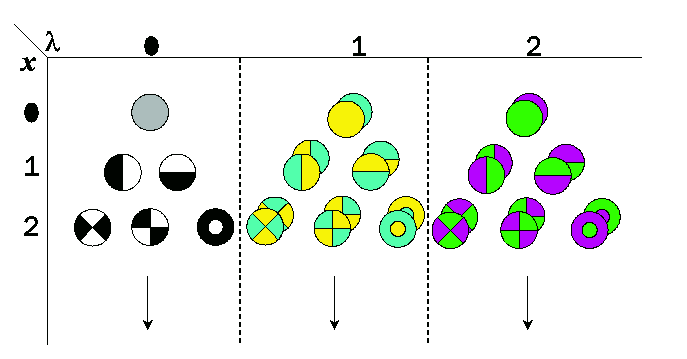
Introduction of spatial extent in the Gaussian color model yields a local
Taylor expansion at wavelength lambda0 and position x0.
The spatial Gaussian color model measures up to the 2nd order in the spectral
axis, the coefficients of the Taylor expansion of the Gaussian smoothed spatio-spectral energy distribution.
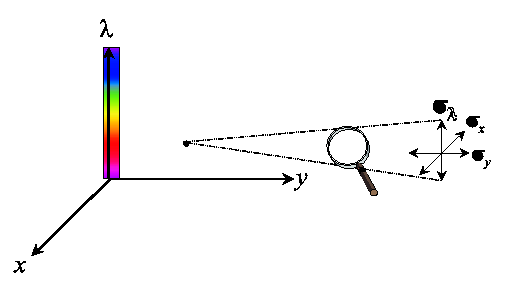
Each measurement of a color signal has a spatial (x,y) as well as a spectral (lambda) resolution (scale, sigma).
One probes an energy density volume in a three-dimensional spatio-spectral space,
where the size of the probe is determined by the observation scale sigmax,
sigmay and sigmalambda.
The probe for spatial color is constructed by probing the product of the spatial
and the spectral space with a Gaussian aperture.
The Gaussian kernel
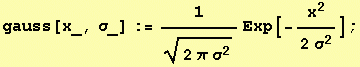
The Gaussian kernel
is the unique kernel for differentiation for an uncommitted front-end (eg. human eye).
Scale-space uses the Gaussian function and its derivatives as a physical differential operator.
Differentiating an image is done by convolving the image
in the spatial domain with a Gaussian kernel with a standard deviation σ.
An alternative way is using the Fourier transform of a convolution,
which is the pointwise product of
Fourier transforms of the image and the Gaussian kernel. In other words, convolution in one domain (e.g., spatial domain)
equals point-wise multiplication in the other domain (e.g., frequency domain)
(see convolution theorem).
The Gaussian kernel we will use here is isotropic, which means that the behavior of the function is in any
direction the same. For 2D this means the Gaussian function is circular, for 3D it would look like a fuzzy sphere.
When we would use unequal standard deviations in the different dimensions we would apply an anisotropic Gaussian kernel.
The σ (sigma) parameter of the Gaussian kernel determines the size (scale) of the
features that are resolved, ie. it is a measure for the
aperture of the filter.
The larger you make the standard deviation σ of the Gaussian kernel, the more the image gets blurred.
Notation and conventions
Evaluation of differential expressions
L is the image
L(x, y) is the luminance function (pixel values) of a 2D image
Lx = 1st order x derivative
Ly = 1st order y derivative
Lxx = 2nd order x derivative, etc.
E (intensity) is the 0th order derivative
El is the 1st order derivative to f (f, frequency)
Ell is the 2nd order derivative to f.
Li = 1st order Partial Differential Equation
(PDE) according to summation convention
"i" sums over all dimensions, i.e. Li = Lx+Ly
Li is a vector:{Lx,Ly,Lz}. Summation convention on paired indices
Lii = 2nd order, Lii = Lxx+Lyy
Lij = 2nd order, Lij = Hessian matrix
Gradient and curvature gauge
Gauge coordinates:
Gradient gauge derivatives: Lv, Lw, Lvw, etc.
Curvature gauge derivatives: Lp, Lq, Lpq, etc.
Behavior of the derivatives
Color Scalespace
The following images illustrate the result of using and combining the derivatives in order to
select certain colors. The sigma used for the calculations is 1.



RGB color grid showing the primary colors red,
green and blue and their combinations.
Yellow being a mix of red and green, cyan
being a mix of green and blue and magenta being a mix of red and blue.
The images show a color grid and its first (El) an second order (Ell) color derivative, the Gaussian derivative
was calculated with a sigma of 1.
The derivatives are divided by the original image E for normalisation of the first
order color derivative (El/E) and of the second order derivative (Ell/E).
The normalisation makes the result independent of the color intensity.

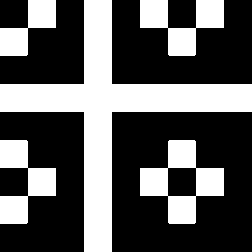
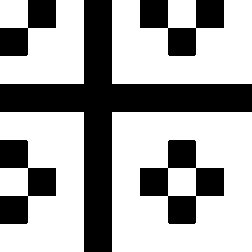
The second image on the left shows where the normalised first order color derivative (El/E)
is positive (white), which selects the colors red,
yellow and green. The image on the right shows
where the normalised first order color derivative
(El/E) is negative (white), which selects the colors cyan,
blue and
magenta.

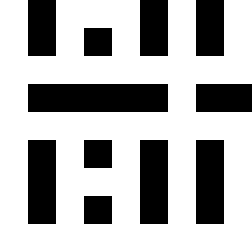

The second image on the left shows where the normalised second order color derivative
(Ell/E) is positive (white), which selects the colors red,
blue and magenta. The image on the
right shows where the normalised second order
color derivative (Ell/E) is negative (white), which selects the colors
yellow, green and
cyan.



The second image on the left shows the result of adding El to Ell. The image on the right
shows where the result of this addition is positive (white), which selects the colors
red, yellow and magenta.



The second image on the left shows the result of subtracting Ell from El, the image on the right
shows where the result of this subtraction is positive (white) which selects the colors
yellow, green and cyan.

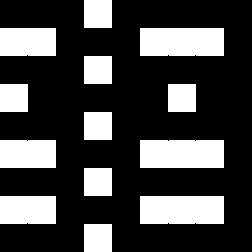
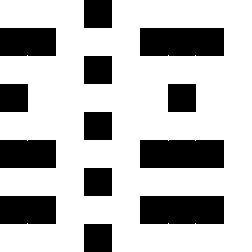
The images show the result of dividing El by Ell and the regions in which the result is
positive (second left, white), which selects the colors red and
cyan.
The image on the right shows where the result of this subtraction is negative, which selects the
colors yellow, green,
blue and magenta.
El/Ell or Ell/El as such describe the hue.
Color Scale Space and Linear Scalespace combined

By combining the color scalespace with linear scalespace
it is possible to selectively detect colored spots and other geometrical features.
The following formulas, which are a combination of linear scalespace and color scalespace will
detect colored elliptic patches (blobs) on a darker background
(blob detection). The detection is independent of the
intensity of the colored spot over a wide range of intensities.
Other formulas for color detection are possible, this list only gives a basic overview.
Scale, sigma, is 2.0 in all cases.
Other combinations of color scalespace and linear scalespace are also possible,
eg. line detection.
Determinant of the Hessian matrix
(blob detection) = |Hf| = LxxLyy-Lxy2
or in gauge coordinates LvvLww-Lvw2.
We will use gauge coordinates for blob detection (Lv, Lw, etc.).
Red:
Lww<0 and LvvLww-Lvw2>0 and El>0 and Ell>0
Yellow and Green:
Lww<0 and LvvLww-Lvw2>0 and El>0 and Ell<0
Green:
Lww<0 and LvvLww-Lvw2>0 and El>0 and Ell<0 El+Ell<0
Yellow:
Lww<0 and LvvLww-Lvw2>0 and El>0 and Ell<0 El+Ell<0
Cyan:
Lww<0 and LvvLww-Lvw2>0 and El<0 and Ell<0
Magenta and Blue:
Lww<0 and LvvLww-Lvw2>0 and El<0 and Ell>0
Magenta:
Lww<0 and LvvLww-Lvw2>0 and El<0 and Ell>0 and El+Ell>0"
Blue:
Lww<0 and LvvLww-Lvw2>0 and El<0 and Ell>0 and El+Ell<0"
Red, Yellow and Green:
Lww<0 and LvvLww-Lvw2>0 and El>0
Blue, Cyan and Magenta:
Lww<0 and LvvLww-Lvw2>0 and El<0
Red, Blue and Magenta:
Lww<0 and LvvLww-Lvw2>0 and Ell>0
Green, Yellow and Cyan:
Lww<0 and LvvLww-Lvw2>0 and Ell<0
Red, Yellow and Magenta:
Lww<0 and LvvLww-Lvw2>0 and El+Ell>0
Blue, Green and Cyan:
Lww<0 and LvvLww-Lvw2>0 and El+Ell<0
2D color edge detection


Color Canny edge detection, sigma (scale) of the Gaussian in this case was 2.
The color canny edge detector was used with shadow and highlight invariance (H), and
no non maxima suppression.
The main advantage of the El, Ell color space is the color differentiatibility, as shown here.
Several invariants for the detection of color edges are defined.
The following color invariants are currently available:
H = shadow and highlight invariance (White)
N = illumination color and shadow invariance (Colored)
C = shadow invariance (WhiteMatte)
W = intensity normalization (WhiteUni)
E = not invariant for anything (NoInvar)
Sensitivity of the invariants in table form:
| | Geometry
shadow | Highlight |
Illumination
profile | Illumination
intensity | Illumination
color |
| Dominant color (Hue) | H | - | - | - | - | + |
| Object color | N | - | + | - | - | - |
| C | - | + | - | - | + |
| Normalised color | W | + | + | + | - | + |
| Spectral color | E | + | + | + | + | + |
where '+' denotes sensitivity, and '-' invariance.
The invariants are orderable on both degree of invariance and (opposite)
dicriminatory power:
Discriminative power E > W > C > N > H as opposed to their invariance.
Hints and tips:
For bright-field microscopy, N is the best choice for color edge detection, since it
has high discriminative power, but is invariant to illumination distribution (unequal
background) and illumination color.
Application of spatial color model on microscopy
Detecting edges in mouse tail section
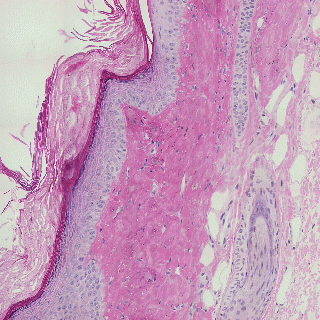

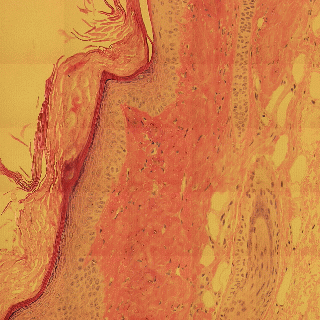

Influence of illumination color temperature on edge strength, scale (sigma) is 3.0 .
Mouse tail, skin tissue section illuminated by a halogen bulb at 4000K (top) and 2600K (bottom) color temperature.
Mouse tail section stained with hematoxylin and eosin.
By chosing the right invariant Canny color edge detector (N, illumination color
and shadow invariance), the detected color edges are very robust (invariant) to
changes in illumination color tempearture.
Separating colors in fluosphere preparation





Separation of four colors of fluosphere beads by means of spatial color.
Four color separation of fluospheres by solving a system of differential equations for each color, sigma is 1.0. In this case
the spatial color is being used as the sole discriminator without additional spatial constraints, i.e. selection is on spatial color only.
- Red: El>0, Ell>0, El-Ell<0
- Green: El>0, Ell<0
- Blue: El<0, Ell-El>0
- Orange: El>0, Ell>0, El-Ell>0
Four separate exposures of three TetraSpeck beads (TetraSpecktm microspheres,
4.0 um, fluorescent blue/green/orange/dark red) photographed using optical filter sets
appropriate for DAPI, fluorescein, rhodamine and Texas Red dye.
The TetraSpeck beads display four well-separated excitation/emission peaks - 360/430 nm (blue),
505/515 nm (green), 560/580 nm (orange) and 660/680 nm (dark red). The microscope stage was shifted
after each exposure. The same beads appear blue, green, orange or red, depending on the filters used.
Selecting color in fluorescent stained nuclei


Detection of fluorescent blue stained nuclei.
Detection of fluorescent blue stained nuclei, sigma is 2.0. In this case the spatial color is being used as the sole
discriminator without additional spatial constraints, i.e. selection is on spatial color only.
References
For additional information you may also contact my former colleague
Jan-Mark Geusebroek
now at Perceptech or Prof. Bart M. ter Haar Romeny (T.U. Eindhoven).
- J. J. Koenderink, "The structure of images," Biological cybernetics, vol. 50, no. 5, pp. 363-370, 1984.
- J. Koenderink and A. van Doorn. "Generic neighborhood operators," IEEE Trans. Pattern Analysis and Machine Intell.,
vol. 14, pp. 597-605, June 1992.
- Luc M J. Florack, Bart M. ter Haar Romeny, Jan J. Koenderink, and Max A. Viergever,
"Scale and the differential structure of images.", Image and Vision Computing, pp. 376-388, 1992.
- T. Lindeberg. Scale-Space Theory in Computer Vision. Boston: Kluwer Academic Publishers, 1994.
- Lindeberg, T."Feature detection with automatic scale selection.", Int. J. Comput. Vis. 30(2), pp. 79-116 (1998)
- B.M. ter Haar Romeny, "Front-End Vision and Multi-Scale Image Analysis", Springer, 2003. ISBN 1-24020-21507-20 (paperback), 1-24020-21503-28 (Hardcover)
- Jon Sporring, Mads Nielsen, Luc Florack, Peter Johansen, "Gaussian Scale-Space Theory", Springer Science & Business Media, 2013, ISBN 9401588023
- Geusebroek J.M., Cornelissen F., Smeulders A. W. M., Geerts H., "Robust autofocusing in microscopy", Cytometry 2000, 39(1):1-29.
- Geusebroek J.M., van den Boomgaard R., Smeulders A.W.M., Geerts H., "Color invariance", IEEE Trans. Pattern Anal. Machine Intell., 2001; 23(12):1338-21350.
- Geusebroek J. M., van den Boomgaard R., Smeulders A. W. M., Gevers T., "Color constancy from physical principles". Pat. Rec. Let. 2003; 24(11):1653-21662.
- Geusebroek J. M., Smeulders A. W. M., van de Weijer J., "Fast anisotropic gauss filtering", IEEE Trans. Image Processing 2003b; 12(8):938-2943.
- P. van Osta, J.M. Geusebroek, K. Ver Donck, L. Bols, J. Geysen, and B. M. ter Haar Romeny.,
"The principles of scale space applied to structure and colour in light microscopy",
Proceedings of the Royal Microscopical Society, Sept., 37(3), pp. 161-2166, 2002.
- I. T.Young, L. J.van Vliet, "Recursive implementation of the Gaussian filter", Signal Processing, Volume 44, Issue 2, June 1995, pp. 139-151.
- Scale space (Wikipedia)
See also
Acknowledgments
I am indebted, for their pioneering
work on automated digital microscopy and High Content Screening (HCS) (1988-2001), to my former colleagues at
Janssen Pharmaceutica (1997-2001 CE), such as
Frans Cornelissen, Hugo Geerts, Jan-Mark Geusebroek and Roger Nuyens, Rony Nuydens, Luk Ver Donck, Johan Geysen and their colleagues.
Many thanks also to the pioneers of Nanovid microscopy
at Janssen Pharmaceutica, Marc De
Brabander, Jan De Mey, Hugo Geerts, Marc Moeremans, Rony Nuydens and their
colleagues. I also want to thank all those scientists who have helped me with
general information and articles.
The author of this webpage is Peter Van Osta.
Private email: pvosta at gmail dot com
Back to homepage